Дельта -функція, δ-функція, функція Дірака — це узагальнена функція, формально визначається як неперервнийлінійний функціонал у просторі диференційовних функцій. δ-функція не є функцією в класичному розумінні.
Введена англійським фізиком Діраком. Дозволяє записати просторову густину фізичної величини (маса, електричний заряд, інтенсивність джерела тепла, сили тощо) зосередженою або прикладеною в одній точці. Наприклад, густина точкової маси m, що знаходиться в точці  , евклідового простору
, евклідового простору  , записується за допомогою δ-функції у вигляді
, записується за допомогою δ-функції у вигляді  .
.
 , евклідового простору
, евклідового простору  , записується за допомогою δ-функції у вигляді
, записується за допомогою δ-функції у вигляді  .
.
Одномірна функція Дірака
Функція Хевісайда, H, — це розривна функція дійсної змінної значення якої рівне 0 для від'ємних значень аргумента і рівне 1 для додатніх значень аргумента. В більшості випадків значення функції в точці нуль H(0) не є важливим. Функція названа на честь англійського математика Олівера Хевісайда і широко використовується в теорії керування і обробці сигналів. В теорії ймовірностіфункція Хевісайда з 'H(0)=1 є функцією розподілу випадкової змінної, що майже напевно рівна нулю.
Функція Хевісайда є первісною дельта-функції Дірака і можна записати.
В даній рівності зміст інтегрального виразу залежить від концепції узагальнених функцій, що використовується і рівність може не справджуватися в нулі.
Функция  ,
,называется единичной функцией Хевисайда и обозначается через

 Миттєве прискорення[ред. • ред. код]
Миттєве прискорення[ред. • ред. код]
двомірна функція Дірака
Означення[ред. • ред. код]
δ-функція визначається формальним співвідношенням
для будь-якої неперервної функції  .
.
 .
.Властивості[ред. • ред. код]
Для дельта-функції однієї змінної справедливі такі рівняння:
 .
. .
.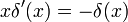 .
. , де
, де 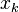 — нулі функції
— нулі функції  .
.
Інтегральне представлення[ред. • ред. код]
У багатьох випадках зручним виявляється таке представлення дельта-функції:
Розглянемо інтеграл
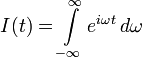 , (1)
, (1)
який можна інтерпретувати як границю
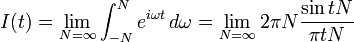 . (2)
. (2)
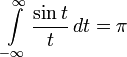 . (3)
. (3)
Як наслідок з (3) для будь-якого 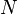 справедлива рівність:
справедлива рівність:
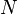 справедлива рівність:
справедлива рівність: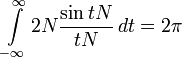 . (4)
. (4)
Можна показати, що при необмеженому зростанні  виявляються правильними всі властивості дельта-функції і функція (2) прямує до
виявляються правильними всі властивості дельта-функції і функція (2) прямує до  ; це дозволяє зробити висновок, що:
; це дозволяє зробити висновок, що:
 виявляються правильними всі властивості дельта-функції і функція (2) прямує до
виявляються правильними всі властивості дельта-функції і функція (2) прямує до  ; це дозволяє зробити висновок, що:
; це дозволяє зробити висновок, що: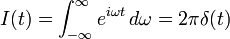 .
.
Похідна дельта-функції[ред. • ред. код]
Фундаментальний вираз, що описує похідну дельта-функції 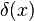 :
:
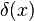 :
:![\int f(x)\delta^{[n]}(x)\,dx=-\int\frac{\partial f}{\partial x}\delta^{[n-1]}(x)\;dx](http://upload.wikimedia.org/math/6/4/9/649b6072b77c419cfc30e9b183e61bd4.png) .
.
Підставивши 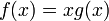 , одержимо вираз:
, одержимо вираз:
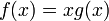 , одержимо вираз:
, одержимо вираз:![\int xg(x)\delta^\prime (x)\;dx=-\int\delta(x)\frac{\partial}{\partial x}[xg(x)]\;dx](http://upload.wikimedia.org/math/d/2/0/d20015f5751f2a845e5dab2110ba2e01.png) .
.
Після перетворення маємо:
![-\int\delta(x)[g(x)+xg^\prime(x)]\;dx=-\int g(x)\delta(x)\;dx](http://upload.wikimedia.org/math/b/1/e/b1e7a682aee4783828e599981f992213.png) .
.
Оскільки 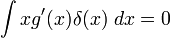 , одержуємо остаточний вираз
, одержуємо остаточний вираз
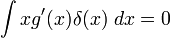 , одержуємо остаточний вираз
, одержуємо остаточний вираз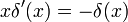 .
.
У загальному вигляді вираз похідної дельта-функції записується так:
![\int [x^{n}f(x)]\delta^{n}(x)\;dx=(-1)^{n}\int\frac{\partial^{n}[x^{n}f(x)]}{\partial x^{n}}\delta(x)\;dx](http://upload.wikimedia.org/math/f/0/7/f07e77b634c79f1792dec70bdd43d3a8.png) .
.
Для довільної дельта-функції справджуються наступні тотожності:
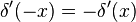 ;
;
 ;
;
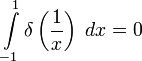 .
.
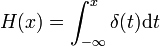

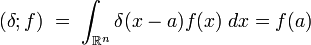
Мојот Сведоштво Здраво на сите. Овде сум за да сведочам како го добив мојот заем од г-дин Бенџамин, откако аплицирав неколку пати од разни заемодавачи кои ветија дека ќе им помогнат, но тие никогаш не ми го дадоа заемот. Додека мојот пријател не ме запозна со г-дин Бенџамин Ли вети дека ќе ми помогне и навистина направи како што вети без никаков облик на задоцнување. Никогаш не мислев дека има уште сигурни заемодаватели додека не се сретнам со г-дин Бенџамин Ли, кој навистина помогна со заемот и ми го смени верувањето. Не знам дали на некој начин имате потреба од оригинален и итен заем, слободно контактирајте го господинот Бенџамин преку WhatsApp 1-989-394-3740 и неговата е-пошта: Lfdsloans@outlook.com ви благодарам.
ВідповістиВидалити