АКСІОМАТИЧНА ПОБУДОВА
АРИФМЕТИКИ.





Формула Бине
Формула Бине выражает в явном виде значение `n`-го числа Фибоначчи `F_n` как функцию от `n`:

где `phi=(1+sqrt(5))/2` — золотое сечение.
При этом `phi` и `(-phi)^(-1)=1-phi` являются корнями характеристического уравнения `x^2-x-1=0`
Формула Бине
Формула Бине выражает в явном виде значение `n`-го числа Фибоначчи `F_n` как функцию от `n`:

где `phi=(1+sqrt(5))/2` — золотое сечение.
При этом `phi` и `(-phi)^(-1)=1-phi` являются корнями характеристического уравнения `x^2-x-1=0`
Суворий систематичний виклад основ теорії деяких спеціальних чисел натурального ряду: фігурних чисел, чисел Мерсенна і Ферма, скоєних і дружніх чисел, чисел Піфагора і Каталана. Описана історія виникнення та основні етапи наукового дослідження зазначених класів натуральних чисел; представлені докази більшості класичних тверджень, пов'язаних з досліджуваними об'єктами, розглянуто ряд менш відомих (але часто не менш цікавих) властивостей і практичних додатків. Крім теоретичної частини, кожен розділ містить великий список завдань, від найпростіших до дуже складних, рішення яких може послужити стимулом до самостійних наукових досліджень у відповідній галузі.

Фгурні числа


Магічний квадрат
Історія
виникнення і еволюції вчення про натуральне число спиралося на властивості
кінцевих множин. Це по суті є історія розвитку числення на пальцях, на
рахунках, на абаках різного вигляду, словом, - на конкретних множинах.

Виклад шкільної
арифметики з понять теорії кінцевих множин почав німецький математик Фрідріх
Мейєр,
співробітник відомого німецького математика Георга Кантора по
створенню теорії множин, в своєму підручнику 1885 р.
В Радянському
Союзі, це зробив професор І. К. Андронов
в своїх підручниках арифметики 1951 і 1955 рр. («Арифметика натуральних чисел»
і «Арифметики дробових чисел і основних величин»).
Природно виникає
питання: з яких первинних тверджень можна вивести все вчення про натуральне
число без посилань на наочність? Іншими словами слід встановити, які твердження арифметики натуральних чисел потрібно прийняти без
доведення, щоб з них можна було вивести всі інші теоретичні положення.
Твердження, що
приймаються без доведення, отримали вже в давнину назву аксіом. Вперше цей термін
зустрічається у Арістотеля для позначення загальновизнаних положень. У Евкліда
немає терміну аксіома,
а твердження, що приймаються без доведення, називаються загальними поняттями.
Отже, в ХІХ столітті виникло питання про
аксіоми арифметики натуральних чисел.
У Греції з
математичних наук раніше інших розвинулася геометрія. У ній виникло перш за все
питання про аксіоми і заснованому на аксіомах – аксіоматичному – побудові
геометрії.
Питання це у
вельми доконаному для свого часу виді був вирішено Евклідом (близько 300 р. до
н. е.). «Начала» Евкліда протягом двадцяти з лишком століть вважали зразком
логічної побудови системи науки на підставі вибраної системи аксіом. Евклід дає на початку викладу перелік
визначень, вимог (постулатів) і «загальних понять» (аксіом), а потім велике
число теорем,
тобто тверджень, які доводяться в
основному на базі аксіом і постулатів. Для Евкліда аксіоми – це самоочевидні
істини.
Проте серед
аксіом і постулатів у Евкліда була пропозиція, яка здавалася іншим авторам
недостатньо очевидним. Це аксіома (або постулат), який у Евкліда звучить так: «Якщо пряма, падаюча на дві прямі (що перетинає їх), утворює
внутрішні і по одну сторону кути менше (у сумі) двох прямих кутів, то
необмежено продовжені ці дві прямі зустрінуться на тій стороні, де кути менше
два прямих».
Це пропозиція
тим, що продовжують Евкліда не представлялася очевиднішою, ніж багато з тих
пропозицій, які доводяться.
Робилися
численні спроби перетворити цю пропозицію на теорему виведенням його з інших
аксіом, тобто довести постулат Евкліда, але всі ці спроби виявилися
безрезультатними. Великий російський вчений Микола Іванович Лобачевський (1792–1856
рр.) довів, що пропозиція Евкліда дійсно є аксіомою – пропозицією, яку не можна
вивести з інших аксіом Евкліда. Лобачевський побудував нову геометрію, в якій
всі пропозиції до постулату Евкліда або що розглядаються незалежно від нього
викладені в системі розвитку евклідової геометрії, але всі чужорідні по
відношенню до ним пропозиції видозмінюються.
Геометрія Н. І.
Лобачевського послужила початком великій кількості неевклідової геометрії.
Висновки геометрії Лобачевського у багатьох випадках носять абсолютно
парадоксальний характер і суперечать нашим звичайним поглядам на речі, але
серед них немає жодного, безглуздість якого могла б бути встановлена.
Звідси витікає
погляд, згідно якому аксіомами є не тільки самоочевидні істини, але взагалі
пропозиції, що приймаються нами без доказу. Нова геометрія Лобачевського,
побудована на його системі аксіом, десятки років не отримувала визнання і
називалася уявною. Проте в XX в. вона стала важливим знаряддям сучасної науки
про природу (астрономії, фізики), особливо в області руху. Даючи таким, що
вчиться визначення аксіоми, як пропозиції, що приймається без доказу, вчителеві
слід пов'язувати це з доступним викладом поглядів великого ученого і
революціонера в науці М. І. Лобачевського.
У розвитку
арифметики і алгебри XIX в. спостерігалися явища, подібні викладеним для
геометрії.

Ірландський
математик Джордж Буль (1815– 1864
рр.) близько 1850 р. видав декілька книг по логіці і математиці, в яких
висловлюється деяка нова арифметика (алгебра), що йде різко в розріз із відомою
на той час арифметикою. У основі її лежить система аксіом, серед яких, окрім
ряду тверджень звичайної арифметики (наприклад, а + b = b + а, аb = bа і ін.),
є і відмінні від аксіом звичайної арифметики, наприклад, така: (а + b) ∙ (а + с)
= а + bс і ін.
Нову арифметику
розглядали як гру з символами, позбавлену якого б то не було практичного сенсу.
Проте в даний час ті електронні рахункові машини, про які мовилося в попередніх
розділах, побудовані на підставі цієї незвичайної арифметики Буля, такої, що
називалася довгий час безглуздою.
Незабаром після
появи роботи Буля було поставлено питання про систему аксіом, які лежать в основі
звичайної («застосовною») арифметики. Таким чином, питання про систему аксіом
арифметики було вирішене в 1889 р.

Система аксіом арифметики, встановлена
італійським математиком Пеано (1858-1932 рр.) і прийнята в даний час
наукою, складається з чотирьох тверджень:
1. Одиниця є натуральне число, не наступне безпосередньо ні за яким
натуральним числом, іншими словами: одиниця
є перше число натурального ряду.
2. За кожним натуральним числом а безпосередньо слідує одне і лише одне натуральне число а', що дорівнює а+1.
3. Кожне натуральне число а,
відмінне від 1, має одне і лише одне натуральне число, за яким число а безпосередньо слідує.
4. Якщо яке-небудь твердження: а) справедливо для n = 1 (або n
= 0) і б) якщо з припущення про
справедливість цього твердження для довільного натурального числа n слідує
справедливість його для числа n+1, то це твердження вважається справедливим для
довільного натурального числа.
Якщо визначити ще арифметичні дії
додавання та множення як рівності:
а + (b + 1) = (а + b) + 1, а∙(b + 1)= аb + а,
то всі правила
арифметики натуральних чисел можуть бути виведені з вказаних чотирьох аксіом.
Таке визначення
дій додавання і множення натуральних чисел було введене вперше чеським
математиком Больцано(1781 – 1848 рр.) в 1810 р.
Потім незалежно
від нього німецьким шкільним вчителем, геніальним математиком Грассманом
(1809–1877 рр.) в 1861 р. і ще раз незалежно від попередників німецьким
математиком Ганкелем (1839 – 1873 рр.) в 1869 р.
Унаслідок того,
що роботи Больцано довгий час залишалися невідомими широкому загалу і майже забутими,
аксіоматична побудова арифметики зазвичай зв'язується з іменами Грассмана і Ганкеля,
що є безперечною помилкою. Незалежно від робіт Больцано і раніше робіт
німецьких математиків почав виявлення аксіом арифметики М. І. Лобачевський
(Алгебра або числення кінцевих, 1834 р.).

До цих імен треба приєднати ще ім'я
німецького ученого Фреге (1848–1925
рр.).
Він з 1879 р. детально розвивав ті ж ідеї, які висловив
свого часу Больцано, але і вони
залишилися непоміченими в науці.
Роботи Буля,
Фреге і Платона Сергійовича Порецького (1846 – 1907 рр.) представляють основу
науки математичної логіки, в області якої в даний час відбувається вельми
інтенсивна робота. Питання про аксіоми арифметики виявилося надзвичайно
складним і важким. Ідеї Больцано, Буля,
Порецького і Грассмана на
протязі десятилітті залишилися незрозумілими.
Ретельно розроблене учення Готлоба
Фреге добилося визнання математиків тільки в 1903 р.
Складність
питання про аксіоматичне обгрунтування арифметики ілюструється, між іншим,
наступним фактом: австрійський математик і логік Курт Гедель (народився в 1906 р. в Чехословакії) в 1932 р. довів
засобами математичної логіки теорему:
у будь-якій системі аксіом виникають
питання, які даними цієї системи не можуть бути розв’язані.
Ця теорема є
одним з актуальних питань філософії математики сьогоднішнього дня.
Однією з
основних особливостей математики наших днів є аксіоматична побудова її. З
попередніх рядків ми знаємо, що сучасний погляд на аксіоми виробив М. І. Лобачевський.
Ми можемо з
гордістю констатувати факт, що М. І. Лобачевський був не тільки реформатором
геометрії, що визнається всім світом вже давно, але і революціонером в області
математики в цілому. Лобачевський є першим вчителем аксіоматичної математики XІX
ст.
Учень не повинен
на підставі цих фактів приходити висновку, що справжньою науковою арифметикою є
тільки арифметика, яка логічно
побудована з аксіом, і все, що було накопичене людством до такої побудови в
арифметиці, є первинним примітивним матеріалом для справжньої науки. «Для
математики, що розвивається, логіка є гігієною, але вона не поставляє їй їжі, варто
зрозуміти, що насущним хлібом, яким математика живе, є завдання, які потрубують
зання на практиці», – пише відомий французький математик А. Вейль
(«Майбутнє математики»).
Теми для досліджень
1.1. Історія питання
1.2. Визначення і формули плоских фігурних чисел
1.3. Цікаві закономірності плоских фігурних чисел
1.4. Знаходження квадратних чисел, які є трикутними
1.5. Задача Ейлера про кількість вмісту даного числа у всіх багатокутних числах
1.6. Центральні багатокутні числа
1.7. Просторові фігурні числа
1.8. Про роль фігурних чисел в математиці
1.9. Завдання
Література до розділу 1
2. Числа Мерсенна і Ферма
2.1. Прості числа. Способи перевірки простоти числа
2.2. Формули простих чисел
2.3. Числа Ферма. Історія питання
2.4. Найпростіші властивості чисел Ферма
2.5. Методи перевірки простоти чисел Ферма
2.6. Числа Ферма. Невирішені проблеми
2.7. Числа Мерсенна. Історія питання
2.8. Елементарні властивості чисел Мерсенна
2.9. Визначення простоти чисел Мерсенна
2.10. Числа Мерсенна. Невирішені проблеми
2.11. Завдання
Література до розділу 2
3. Досконалі і дружні числа
3.1. Історія питання
3.2. Арифметичні функції τ(n) і σ(n)
3.3. Парні досконалі числа. Формула Евкліда-Ейлера
3.4. Непарні досконалі числа
3.5. Найпростіші властивості досконалих чисел
3.6. Надлишкові і недостатні числа
3.7. Узагальнення поняття досконалого числа
3.8. Дружні числа. Правила Сабіта і Ейлера
3.9. Властивості дружніх чисел
3.10. Узагальнення дружніх чисел
3.11. Завдання
Література до розділу 3
4. Числа Піфагора
4.1. Історія питання
4.2. Примітивні піфагорові трійки
4.3. Методи генерації піфагорових трійок
4.4. Арифметичні властивості піфагорових трикутників
4.5. Значення сторін піфагорових трикутників
4.6. Піфагорові трикутники із загальними елементами
4.7. Піфагорові трикутники-близнюки
4.8. Піфагорові трикутники, сторони яких є квадратами
4.9. Піфагорові трикутники і точки площині
4.10. Героновы трикутники
4.11. Піфагорові четвірки
4.12. Велика теорема Ферма
4.13. Завдання
Література до розділу 4
5. Числа Каталана
5.1. Історія питання
5.2. Визначення чисел Каталана
5.3. Властивості чисел Каталана
5.4. Задачі, що приводять до числа Каталана
5.5. Послідовність Каталана та інші спеціальні комбінаторні числа
5.6. Трикутник Каталана
5.7. Завдання
Література до розділу 5
Несомненно, самым замечательным математическим фактом является тождество 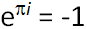 .
.
 .
.
Немає коментарів:
Дописати коментар