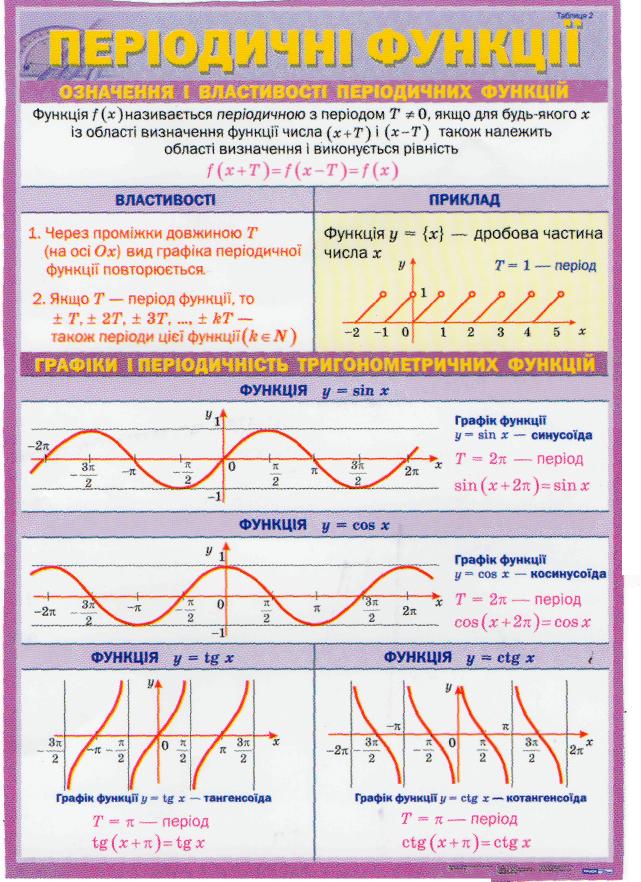
ПЕРІОДИЧНІ ФУНКЦІЇ

Означення. Функція називається періодичною з періодом Т ≠ 0, якщо для будь-якого х з області визначення числа х + Т та х – Т також входять до області визначення і виконується рівність :
f (х + Т) = f(х – Т)=f(х).
де дійсне число Т ≠ 0 і хє D(y).
Приклади. А) Функція
ант’є у = [x] – неперіодична функція на всій області визначення, бо можна вказати(або
існує хоча одне ) таке значення х із області визначення, що f (х + Т) ≠
f(х –
Т) ≠ f(х).
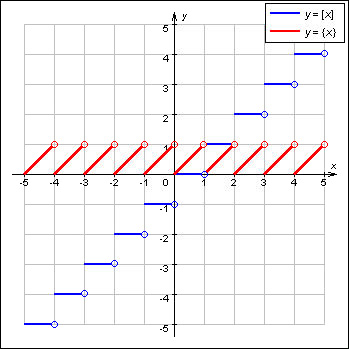
Б) Функція мантиса у = {x} – періодична функція на всій області визначення,
бо можна вибрати довільне значення х
із області визначення, що f (х +
Т) = f(х –
Т) = f(х). Період Т = 1.
Cпосіб знаходження періоду
функції мантиса. Дійсно, згідно
означення функції, для довільного значення х
із області визначення:
f (x)= {x} = х - [x];
f (x + 1) = {x + 1} = х
+ 1 - [x +1].
Зауважимо, що [x +1] = [x] + 1. Тому для довільне значення х із області визначення,
f (x + 1) = {x + 1} = х
+ 1 - [x] -1 = х - [x] =
f (x);
f (x + 1) = f (x),
що і треба було
довести.
В) Постійна
функція у = 3 – періодична функція на всій області визначення, бо можна
вказати таке значення х із області визначення, що f (х +
Т) = f(х –
Т) = f(х). Період Т постійної функції це довільне дійсне число. Дійсно,
y(x)=3=3 + 0∙х = 3 + 0∙(х+T)= y(x +Т).
Постійна функція не має найменшого і немає найбільшого
додатного періоду.
Г) Лінійна функція у =
3х -2 – неперіодична функція на всій області визначення, бо можна вказати
таке значення х із області визначення, що f (х +
Т) ≠ f(х –
Т) ≠ f(х). Це легко переконатися.
Згідно означення періодичної функції, для довільного значення х із області визначення виконується:
3(х +Т)-2 = 3(х -Т)-2;
3х + 3Т - 2 = 3х -3Т-2;
3Т = -3Т;
6Т = 0;
Т =0.
Однак період Т ≠ 0. Тому не існує такого числа Т, щоб виконувалася умова:
Д) Квадратична функція у =
3х2 -х -2 – неперіодична функція на всій області визначення, бо
можна вказати таке значення х із області визначення, що f (х + Т) ≠
f(х –
Т) ≠ f(х).
ПРИКЛАДИ ГРАФІКІВ ПЕРІОДИЧНИХ
ФУНКЦІЙ



Зауваження 1. Згідно даного означення періодичної функції можна
вказувати і від’ємний період функції. На практиці найчастіше потрібно знаходити
найменший додатній період функції Т. Якщо потрібно дослідити і побудувати
графік деякого періодичної функції (наочно зобразити графіком деякий циклічний
процес чи періодичне явище), то спочатку
досліджують і будують графік на
проміжку, довжина якого дорівнює найменшому додатному періоду функції, а потім виконують паралельне перенесення отриманого
графіка на інші проміжки.
Зауваження 2. Якщо f (0 )
– це деяке ненульове дійсне число. Для періодичної функції з найменшим додатнім
періодом Т на всій області визначення можна вибрати такі значення аргумента, де
вона монотонна. Для цих проміжків монотонності визначена обернена функція f
-1 (і це при умові, що f
-1 (0 ) ≠
0) до даної періодичної функції f, тобто виконується рівність:
f (0 )
= f (0 +
Т) = f(0 – Т),
f (0 )
= f (Т)
f -1 f (0)
= Т.
Таким чином, період функції в деяких випадках можна знайти за формулою: Т = f -1 f (0) .
Приклади. Знайдемо періоди і найменший
додатній період тригонометричних функцій:
А)
у = sin x.
Т = f -1 f (0)
= arcsin(sin 0) =0+2pk =2pk , kÎ Z.
Найменший додатній
період синуса, якщо k = 1, то Т = 2p.
Б) у = соs x.
Т = f -1 f (0)
= arccos(cos 0) = 0+2pk =2pk , kÎ Z.
Найменший додатній
період косинуса, якщо k = 1, то Т = 2p.
В) у = tg x.
Т = f -1 f (0)
= arctg (tg 0) =0+pk =pk , kÎ Z.
Найменший додатній
період тангенса, якщо k = 1, то Т = p.
Г) у =сtg x.
Т = f -1 f (0)
= arcctg (ctg 0) = 0+pk =pk , kÎ Z.
Найменший додатній
період, якщо k = 1, то Т = p.
Для кмітливих. Виправте логічну помилку.
Софізм . Для періодичної функції, яка визначена в точці
х =
0, виконується рівність
f (0 )
= f (0 +
Т) = f(0 – Т),
f (0 )
= f (Т)
= f(– Т),
f (0 )
= f (0 +
mТ)
= f(0 +
(1 –m) Т)
= f(nT),
f (mТ) = f(-nТ) = f(0).
Якщо відома обернена
функція f -1 до періодичної функції f,
то
виконується рівність:
f -1 f (Т)
= Т.
Тоді застосуємо
останню властивість, а саме так:
f -1 f (mТ) = f -1
f(-nТ) = f
-1 f(х).
mТ = -nТ = х.
А згідно означення
періодичної функції: Т ≠ 0, Таким чином, періодична функція немає найменшого періоду.
Для юних математиків.
Функції Діріхле  являється періодичною.
Довільне раціональне число є періодом функції Діріхле . Дійсно, сума двох раціональних чисел є
раціональним числом, з іншого боку, сума раціонального і ірраціонального чисел завжди ірраціональна.
являється періодичною.
Довільне раціональне число є періодом функції Діріхле . Дійсно, сума двох раціональних чисел є
раціональним числом, з іншого боку, сума раціонального і ірраціонального чисел завжди ірраціональна.
Отже D(x
+ r) = D(x).
ВЛАСТИВОСТІ ПЕРІОДИЧНИХ ФУНКЦІЙ
Властивість 1. Якщо число Т –
період функції f(х), то число
k∙T (kÎN) також
період цієї функції f(х).
Доведення.
Так як Т
– період функції f(х), то згідно означення маємо таку
рівність:
f (х +
Т) = f(х –
Т) = f(х),
Якщо значення
аргумента вибрати і = х + Т, де х – будь-яке х з області визначення, тоді
отримаємо:
f (і +
Т) = f(і –
Т) = f(і),
f ((х
+ Т) + Т) = f((х – Т) - Т) = f(і),
f (х +
2Т) = f(х –
2Т) = f(х).
Допустимо, що для
натурального числа k
виконується рівність:
f (х + k∙T) = f(х – k∙T) = f(х),
Якщо значення
аргумента вибрати у такому вигляді:
j = х + k∙T,
де х – будь-яке х з
області визначення, тоді отримаємо:
f (j + Т) =
f(j – Т) = f(j).
Тоді отримаємо
f (j + Т) =
f(j – Т) = f ((х + k∙T) + Т) = f((х – k∙T) - Т) =
= f (х +
(k+1)∙T) = f(х –
(k+1)∙T) = f(j).
Таким чином, якщо:
1) х – будь-яке дійсне
число з області визначення D(f),
2) k –
довільне натуральне число,
то має місце
рівність:
Приклад. Функція
мантиса у =
{x} – періодична функція на всій області
визначення, бо можна вибрати довільне значення х із області визначення, що f (х +
Т) = f(х –
Т) = f(х), Ця функція має найменший додатний період Т =
1. Але ця функція має інші періоди:
{x} = {x + 1} = {x +
2∙1} = {x +
3∙1} = {x +
4∙1} = … = {x + k ∙1}
= …,
де k –
довільне натуральне число.
Цікаві факти. Складена функція у
=f({x}) – періодична з періодом Т = 1 і на відрізку
[0; 1] має властивість f(x) =f({x}). Для побудови її графіка варто виконати такі дії:
а) побудувати графік на відрізку від нуля до одиниці; б) паралельно перенести
цей графік вліво і вправо на одиничні проміжки.
Цікаві факти. Якщо періодична функція має період Т, то
вона має нескінчену множину періодів:
{…, - n∙T, …, -4∙T,
-3∙T, -
2∙T, -T, T, 2∙T, 3∙T, 4∙T , …
}.
Означення. Найменший з додатних періодів, якщо він існує, називається основним періодом періодичної функції.
Наслідок. Якщо функція має основний період, то будь-який інший період кратний до
основного.
Властивість 2. Якщо число Т – ненульовий період функції f(х), то функція , що являється лінійною комбінацією цією функції із лінійним
комбінацією аргумента
у = А f(mх+n)+В
де А , m, n,
В – постійні дійсні числа.
також є періодичною і
її період дорівнює частці T:| m|, m
≠ 0.
Властивість 3. Якщо число Т –період функції f(х), то складена функція
у = g( f(х)) також є періодичною і її період дорівнює T, але він можливо і не найменший за абсолютною
величиною.
Властивість 4.
Графік періодичної функції з
періодом Т (Т>0)/ можна розрізати на довільну кількість рівних фігур.
Щоб розрізати на
довільну кількість рівних фігур, для
цього досить знайти значення функції на кінцях відрізку довжиною Т. Множина точок {(m; f(m)): mÎ[х, х+Т ]}- рівні фігури на
графіку періодичної функції.
Щоб на графіку
періодичної функції знайти рівні фігури варто спочатку дослідити і побудувати
графік періодичної функції (цей графік є наочним зображенням деякого циклічного
процесу чи періодичного явища) на
проміжку, довжина якого дорівнює найменшому додатному періоду функції, а
потім виконати паралельне
перенесення цієї фігури уздовж осі Ох
отриманого графіка на відстань n∙T ліворуч і праворуч.
Властивість 5. Період
алгебраїчної суми періодичних функцій з спільними періодами дорівнює найменшому
спільному кратному періодів усіх доданків, за виключенням подібних членів, сума
яких після зведення рівна нулю.
Властивість 6. Періодичні функції не мають похилих та
горизонтальних асимптот.
Зауваження1. Виявляється, що якщо у двох періодичних функцій немає спільних
періодів, то їх сума, різниця, добуток можуть бути неперіодичними!
Наприклад: у = sin(px) + sin3x; у = sin(px)∙sin3x;
Зауваження2. Виявляється може бути
періодичною функція, що є сумою періодичної і неперіодичної функції.
Наприклад, у = sin(px) + sin3x + (- sin3x);
Зауваження3. Для доведення неперіодичності
функції досить показати, що вона неперіодично повторює яку-небудь
властивість даної функції.
Приклади cкладених
неперіодичних і періодичних функцій.
2. Функція y = sign(sin(px)) – періодична з найменшим додатним періодом Т= 2.
3. Функція
y = sign(tg(px)) – періодична з найменшим додатним
періодом Т= p.
4. Функція y = {x}2
– періодична з найменшим додатним періодом
Т= 1.
5. Функція y = {x}0,5
– періодична з найменшим додатним періодом
Т= 1.
6. Функція y = a{x}– періодична з найменшим додатним
періодом Т= 1.
7. Функція y = 1/{x}– періодична з найменшим додатним
періодом Т= 1.
8. Функція y
= cos{x}–
періодична з найменшим додатним періодом
Т= 1.
9.Функція y
= cos x
+ sin x–
періодична з найменшим додатним періодом
Т= 2p.
ЗАПИТАННЯ НА ОСМИСЛЕННЯ ПРОСТОРУ ПЕРІОДИЧНИХ ФУНКЦІЙ
1.
Яка функція являється періодичною?
а)функція ант’є; б) функція мантиса; в)
квадратична; г) лінійна.
2.
Яке число є основним періодом
періодичної функції?
а) найменший із усіх періодів;
б) найбільший із
усіх періодів;
в) найбільший за абсолютною величиною;
г) найменший за абсолютною величиною.
3.
Чи може періодична функція мати тільки один період?
а)може, тільки
нуль; б) не обов’язково; в) не може; г) а)може, тільки не нуль.
4.
Чи вірно, що сума двох періодичних функцій завжди періодична?
а)
так, вірно завжди;
б) не завжди вірно; в) не вірно.
5.
Як знайти період Т різниці двох періодичних функцій f1(x)
- f2(x)?
а) Т =
НСК(Т1; Т2); б) Т = НСД(Т1; Т2); в) Т = mах(Т1; Т2);
г) Т = min(Т1;
Т2).
6.
Чи вірно, що добуток двох періодичних функцій завжди періодична
функція?
7.
а) так, вірно
завжди; б) не
завжди вірно; в) не вірно.
8.
Як знайти період добутку двох різних періодичних функцій з однаковими
основними періодами f1(x) ∙f2(x)?
а) Т = НСД(Т1; Т2); б) Т = Т1=Т2; в) Т = mах(Т1: Т2
; Т1∙ Т2);
г) Т = min(Т1: Т2
; Т1∙ Т2
).
9.
Чи може сума неперіодичних функцій бути періодичною функцією?
а) це завжди
періодична; б) це ніколи неперіодична; в) інколи може.
10.
Відомо, що N(x) – неперіодична функція, а Р(x) - періодична функція. Чи вірно, що складена
функція N(Р(x) ) - періодична?
а)
так, вірно завжди;
б) не завжди вірно; в) не вірно.
11.
Відомо, що N(x) – неперіодична функція, а Р(x) - періодична функція. Чи вірно, що складена
функція Р(N(x) ) - періодична?
а)
так, вірно завжди;
б) не завжди вірно; в) не вірно.
12.
Відомо, що S(x) – періодична функція, а Р(x) - періодична функція. Чи вірно, що функція A∙S(x) + B∙P(x) + C∙Р(x) ∙S(x) - періодична ( А, В, С – ненульові, дійсні
числа)?
а) так, вірно
завжди; б) не
завжди вірно; в) не вірно.
13.
Відомо, що Р(x) – періодична
функція. Чи вірно, що функція
| N(x)| = max{ -1∙Р(x); Р(x) } – періодична?
а)
так, вірно завжди;
б) не завжди вірно; в) не вірно.
14.
Чи вірно, що
періодичні функції не мають похилих та горизонтальних асимптот?
а)
так, вірно завжди;
б) не завжди вірно; в) не вірно.
14.
Відомо, що Р(x) – періодична
функція. Чи вірно, що функція
| N(x)| = Р(x
+ А) – періодична (А, В, С – ненульові, дійсні)?
а) так, вірно завжди; б) не завжди вірно; в) не вірно.
15.
Відомо, що Р(x) – періодична
функція. Чи вірно, що функція
| N(x)| = А∙Р(x)
} – періодична (А, В, С – ненульові, дійсні)?
а) так, вірно завжди; б) не завжди вірно; в) не вірно.
16.
Відомо, що Р(x) – періодична
функція. Чи вірно, що функція
| N(x)| = А∙Р к (x +А) } – періодична (А, к– ненульове дійсне)?
а) так, вірно завжди; б) не завжди вірно; в) не вірно.
17.
Відомо, що Р(x) – періодична
функція. Чи вірно, що функція
| N(x)| = А∙Р (x к +А) } – періодична
(А, к– ненульове дійсне)?
а) так, вірно завжди; б) не завжди вірно; в) не вірно.
Вправи.
1. Встановити відповідність:А) х 1) множина значень функції
Б) у 2) залежна змінна або функція;
В) f 3) область визначення функції;
Г) Т 4) символ закону відповідності;
ґ) D(у) 5) період функції;
Д) Е(у) 6) незалежна змінна або аргумент.
Рівень А
2. Перевірити функції на періодичність. Обґрунтувати
відповідь.
А) 1. y = 5;
2. y = - sin (x+3); 3. y = 2+{x}; 4. y = -2[x];
5. y = |соs x|; 6. y = |sin  |;
7. y = sin |x|; 8. y = сos{x};
|;
7. y = sin |x|; 8. y = сos{x};
Б) 1. y =tg 2x;
2. y = ctg (3x+2); 3. y = соs 0,5x; 4. y = sin( -3-2x);
В) 1. y = {x}2; 2. y =  ; 3. y =
; 3. y = ; 4. y = sin{x} - 3;
; 4. y = sin{x} - 3;
Г) 1. y = [sin x]; 2. y = [cos x]; 3. y = ; 4. y = sin{x}+сos{x}.
; 4. y = sin{x}+сos{x}.
Рівень Б
3. Знайти основний період функцій:
А) 1. y = соs 5х; 2. y = - tg (4x+3); 3. y = соs (2px);
4. y = -{5x};
5. y = |соs3 x|;
6. y = |sin 2x|; 7. y =-3sin|6px|; 8. y = сos{4x};
Б) 1. y = соs 2x+ sin3x;
2. y = 3sin (3x+2)
-4 соs 2x;
3. y = 5соs 0,5x + 2sin( -3-2x);
4. y = 6соs(2+ 4px) + 8sin( 7-2px);
В) 1. y = {4x}2; 2. y =  ; 3. y =
; 3. y = ; 4. y = sin{5px} – tg4px;
; 4. y = sin{5px} – tg4px;
Г) 1. y = |[sin 3x]|; 2. y = [cos 5x]; 3. y = ; 4. y = sin{4px}+сos{5px}.
; 4. y = sin{4px}+сos{5px}.
4. Побудувати графіки, використовуючи періодичність:
1. y = arcos(cos x); 2. y = arcsin(sin x); 3.
y = arcctg(ctg x).
5. Дослідіть на періодичність: y = D(sign(x)))
Запитання з теми «Періодична
функція».
1.
Що означає словосполучення: періодична
функція? Наведіть приклади.
2.
Функція – це закон відповідності,
чи значення, яке вона приймає? Наведіть приклади.
3.
Які є періодичні парні функції при
аналітичному способі задавання? Наведіть приклади.
4.
Якы є періодичні тригонометричні функції при аналітичному способі задавання? Наведіть приклади.
5.
Як задаються обмежені періодичні функції при графічному способі задавання?
Наведіть приклади.
6.
Яка є періодична неперервна функція при аналітичному способі задавання?
Наведіть приклади.
7.
Яка є періодична розривна функція при
аналітичному способі задавання? Наведіть приклади.
8.
Як визначається зростаюча функція
при аналітичному способі задавання? Наведіть приклади.
9.
Як визначається спадна функція при аналітичному способі задавання?
10. Що називають числовою послідовністю? Чи
послідовність із чисел – це функція?
11. Що називають областю визначення функції? Що називають областю значення
функції?
12. Чи вірно, що парні функції ніколи не бувають періодичними?
13. Які обмеження накладають на область визначення
дробово-раціональної функції?






 Тригонометрия
Тригонометрия

 Определение тригонометрических функций
Определение тригонометрических функций
Немає коментарів:
Дописати коментар