Рівняння Баше та його узагальнення

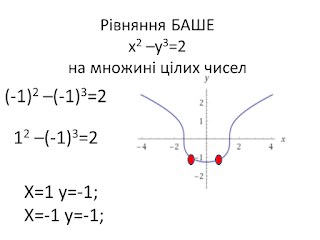
Проблема 1. Чому рівняння Баше x² – y³ = k не має цілих розв’язків, якщо k=-5; k=-6; k=7; k=6?

Узагальнення рівняння Баше

Розглянемо рівняння вигляду

x^2k+1+y^2k = x^2k- y^2k+1

якщо k  - відоме довільне ціле невід’ємне число, (x, y) - пара невідомих цілих чисел.

Розв’язання. Розглянемо випадок, якщо k = 0,  тоді отримаємо:

x¹+y⁰ = x⁰- y¹ ,  якщо x та у – не нульові цілі числа, то  

x+1 = 1- y

x = - y

Отже (x, y) =(m;-m), якщо k = 0,  m – не нульове ціле число, то  

Розглянемо випадок, якщо k  - довільне додатне ціле число,  тоді розділимо однойменні змінні по різним частинам рівняння, отримаємо:

y^2k+1 +y^2k = x^2k- x^2k+1

y^{2k (}у+1) = x^2k(1-х)

Утворимо системи із двох рівнянь:

1)y^2k = x^2k ;   у+1 = 1-х;    тоді (x, y) =(m;-m),

2)y^2k  = 1-х;   у+1= x^2k; тоді  (x, y) =(0;-1),  (x, y) =(1;0),

3)y^2k  = 1;   у+1= x^2k(1-х);  тоді  (x, y) =({mєZ | m^2k(1-m)=2};  1), 

4)у+1=1;  y^2k  = x^2k(1-х); тоді  (x, y) =(0;0),  (x, y) =(1;0),

5) x^2k  = 1;   1-х= y^{2k (}у+1);   тоді  (x, y) =(1;0),

6)1-х=1;   x^2k= y^{2k (}у+1);       тоді  (x, y) =(0;0),  (x, y) =(0;-1).

Безпосередньою перевіркою можна впевнитись, що рівняння має безліч пар-розв’язків, які задовольняють дане рівняння

(x, y) =(0;0), (x, y) =(1;0), (x, y) =(0;-1) та (x, y) =(m;-m),

 якщо k  - довільне додатне ціле число, m - довільне ціле число

Розглянемо випадок, якщо k  - довільне від’ємне ціле число,  тоді розділимо однойменні змінні по різним частинам рівняння і отримаємо, (x, y) =(m;-m), довільне ненульове ціле число.

Відповідь: якщо k< = 0,  то (x, y) =(m;-m); k> 0,  то (x, y) =(m;-m); (x, y) =(1;0), (x, y) =(0;-1).