Класична задача про куркулів

Класична арифметична проблема, напевно, вперше поставлена ​​Евклідом і досліджувалася різними авторами в середньовіччі.

Проблема сформульована як діалог між двома куркулями. Куркуль Мульований каже куркулю Косіокому: "Якщо ти дав мені одне з своїх мішків, я б мав би стільки, скільки ти". Косіокий відповідає: "Якщо б ти віддав мені один з своїх мішків, я мав б удвічі більше, ніж ти". Питання, звичайно, полягає в тому, "Скільки мішків у них є?" Кількість  х мішків у Муля та кількість у мішків Косіока пов'язані з тотожністю:

			(1)
			(2)

які утворюють систему двох лінійних рівнянь. Рішення , .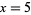

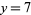Узагальнення 1. Цієї проблеми вивчено Сингмастером (1999, 2002).

 У цій модифікованій проблемі осел каже: "Якщо ти дав мені а  мішків , то я мав би більше у 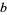 разів, ніж ти", і мул відповідає: "Якщо б ти віддавав свої  с мішків, я мав би більше  y d разів, ніж ти " Це рішення

			(3)
			(4)

які є цілими числами лише тод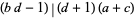і  і .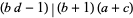
Узагальнення 2. Зустрілись два менеджери різних банків  Прокопенко та Сидоренко. Банкір Прокопенко каже іншому: «Поділи усіх своїх віп-клієнтів  банку на найбільшу кількість груп  з однаковою кількістю клієнтів у кожній групі, в яких не менше 2 клієнтів , і тільки двом групам віп-клієнтів надай фінансовий кеш. Тоді  усі твої клієнти  з твого банку матимуть  вклади в моєму  банку на вигідних відсотках».  Банкір Сидоренко відповідає: «Краще ти  поділи усіх своїх віп-клієнтів банку на найменшу кількість груп  з однаковою кількістю клієнтів у кожній групі, в яких  не менше 2 клієнтів , і тільки двом групам віп-клієнтів надай мій фінансовий кеш. Тоді  усі твої клієнти  з твого банку матимуть  вклади в моєму  банку на вигідних відсотках».  Яка  найменша кількість віп-клієнтів в кожному банку?


Задача для розминки.