Квазіпіфагорове рівняння: gа^2+рb^2=qc^2

 

Приклад. Розв’язати   рівняння Піфагора:

v²  + u² = z²

Розв’язання. Розглянемо трійку чисел:

(v; u; z) =(a^k - b^m;   2a^k/2b^m/2;    a^k + b^m),  

де : v, u, z, невідомі даного рівняння  цілі числа, a, b, - цілі точні квадрати, k, m – цілі числа.

  Покажемо, що ця трійка задовольняє дане рівняння.  

v²+ u² =(a^k - b^m)²+(2a^k^/2b^m/2)²=(a^k)² + (b^m)²-2а^kb^m+4а^kb^m = (a^k)² + (b^m)²+2а^kb^m  = (a^k + b^m)² = z².

Квазіпіфагорові  рівняння – це квадратні рівняння з трьома невідомими вигляду:

gx²+рy² = qz²,

де g, р, q - відомі натуральні числа, g, q – точні квадрати;

x, y, z – невідомі натуральні числа.

Приклади квазіпіфагорових рівнянь: 
А)4x²+7y² = 9z²;

б) 25x²+36y² = 16z².
_______________________________________

Зауваження1. Відоме  піфагорове рівняння: 

x²+ y² = z², 

три числа якого є довжинами сторін деякого прямокутного плоского трикутника.

Зауваження2. У загальному випадку рівняння з трьома невідомими другого степеню можна записувати у вигляді:

а₁x²+ а₂y² + а₃z²+

+а₄xy+ а₅xz+ а₆zy+

а₇x+ + а₈y+ а₉z+а₁₀=0.

Зауваження3. Випадки рівнянь з трьома невідомими або парного, або непарного,  або довільного цілого степеню можна розглядати на множині цілих чисел і записувати у вигляді:

а₁x^2k+ а₂y^2m = а₃z²ⁿ;

b₁x^2k-1+ b₂y^2m-1 = b₃z^2n-1;

c₁x^k+ c₂y^m= c₃zⁿ.
_______________________

Зауваження 4. Нехай n – натуральне число. Як шукати дійсні розв’язки квазірівняння Ферма:

Axⁿ+Byⁿ = Czⁿ,

при умові:

1.                A, B, C - відомі раціональні числа;

2.                x, y, z – невідомі дійсні числа;

3.                у трійки розв’язків (x; y; z), де х, z - два цілих чисел?

Наприклад. Не важко показати, що існує

така трійка дійсних чисел:

 (x; y; z) = ( kA^-1/n;   mB^-1/n;   С^-1/n(kⁿ + mⁿ)^1/n),

де   k, m  – дійсні числа, яка задовольняє рівняння

Axⁿ+Byⁿ = Czⁿ.

Зауваження 5. Нехай n – натуральне число.

Квазірівняння Ферма на множині дійсних чисел можна записувати у вигляді:

AC^-1xⁿz^-n +BC^-1yⁿz^-n = 1,   

або

Pрⁿ + Ggⁿ = 1,      

де р= xz^-1; g= yz^-1;   P= AC^-1;    G= BC^-1.
Додатково: http://fakul-maht10kl.blogspot.com/2017/

Зауваження 6. Нехай a,  b, р, g – дійсні числа, що не дорівнюють 1.

Рівняння на множині дійсних чисел можна записувати у вигляді:

Pр^а+ Gg^b = 1,

 де   р, g – невідомі дійсні числа,   Р, G – відомі дійсні числа. 

 Як розв’язати це рівняння?

Наприклад. Не важко впевнитися, що пара дійсних чисел:

р = (P^-1/a)(1 + m^b)^-1/a, де m – дійсне число;

g =  mG^-1/b(1 + m^b)^-1/b,  де m – дійсне число

утворюють розв’язок рівняння Pр^а+ Gg^b = 1.

На множині цілих чисел розглянемо рівняння:

Аp^x+Вq^y=1.

Якщо А=1,  В=-1, p^x-q^y=1

 то (х; у; p; q)={(2;3;3;2),(2;3;-3;2), (m;0;0;n)}
 тобто 3²-2³=1,  m⁰-0ⁿ=1,
m, n - натуральні числа.

____________________________________________


Наприклад: Довести, що рівняння
x³+y³ = z³ 
має безліч  розв’язків:  (x; y; z), 
де ТІЛЬКИ х, z - два цілих чисел?

Розв’язання.

Нехай  k, m, р – цілі числа. Перевіримо той факт,  що

х = k +m    – це ціле число;

y = (3km²(р² -1) – (1+р³)m³ – 6рk²m)^1/3 – це неціле дійсне число;

z= k-рm – це ціле число;  

задовольняють  дане рівняння: x³+y³ = z³.

Доведення.

x³+y³ = (k +m)³ + ((3km²(р² -1) –(1+р³)m³ -6рk²m)^1/3)³ =

= k³ +3k²m+3km² + m³  + 3km²(р² -1) –(1+р³)m³ -6рk²m =

= k³ -3k²рm + 3kр²m² - р³m³  = (k-рm)³ = z³. Що і треба довести.

Приклад такої трійки-розв’язку з двома цілими параметрами:

(x; y; z)=(k +m;  (9km² – 9m³ – 6k²m)^1/3; k-2m), якщо р=2.

Зауваження 7. Як шукати дійсні розв’язки квазірівняння Піфагора:

Ax²+By² = Cz², 

при умові:

1.                A, B, C - відомі раціональні числа;

2.                у трійки розв’язків (x; y; z), де х, z, у - три цілих чисел?

НАПРИКЛАД. Довести, що рівняння  

gx²+рy² = qz² 

має безліч цілих розв’язків:  (x; y; z), якщо g, q, р – відомі натуральні числа, при цьому g, q – це точні квадрати. 

Доведення. Нехай  k, m – цілі числа. Перевіримо той факт,  що

х = (gk²-рm²)q^0,5 

y = 2kmg^0,5q^0,5  ,

z= gk²+рm²,

задовольняють дане рівняння.

gx²+рy² = (gk²-рm²)²(q^0,5)²  + р(2km)²(q^0,5)²  = qg²k⁴-2рqgk²m²+qр²m⁴+4qрgk²m²= q(g²k⁴+2рgk²m²+4р²m⁴)= q(gk²+рm²)² = qz². Зазначимо, що усі виконані дії з цілими виразами  залишають свої результати у кільці цілих виразів. Що і треба було довести.

Розв’язати в цілих числах рівняння

mx^k+ly^k=-nxy^k,

якщо k, m, l, n  - відомі цілі числа.

Розв’язання. Заміна х на у та заміна у на х  змінює вигляд рівняння,  як являє собою деяку множину точок в декартовій площині. А тому розглянемо випадок, коли розв’язки лежать на прямих  у = pх, які  покривають усю координатну площину хОу. Отримаємо рівняння з одним невідомим:

mx^k+lр^kх^k=-nр^kх^k+1;

(m+lр^k)х^k+nр^kх^k+1=0;

х^k (m+lр^k  + nр^kх)=0;

(m+lр^k  + nр^kх)=0;  х^k=0;

х₁=(-m-lр^k)/nр^k;   х₂=0.

Тоді

у₁=(-m-lр^k)/nр^k-1;   у₂=0.

Накладаємо додаткову умову:

Дробові вирази (-m-lр^k)/nр^k   та   (-m-lр^k)/nр^k-1 – це цілі числа.

Відповідь: ((-m-lр^k)/nр^k; (-m-lр^k)/nр^k-1),  (0; 0).  

Зауваження 8. Існує декілька узагальнень теореми Ферма.

Узагальнення 1 теореми Ферма. Нехай

 a^x+b^y=c^z,    (1)

 де a, b, c, - відомі різні натуральні числа x, y, z – невідомі різні натуральні числа.

Гіпотеза:  Рівняння (1) має безліч розв'язків в натуральних числах.

Узагальнення 2  теореми Ферма.  Нехай

 x^a+y^b=z^c,     (2)

 де a, b, c, - відомі різні натуральні числа x, y, z – невідомі  різні натуральні числа.

Гіпотеза:  Рівняння (2) має безліч розв'язків в натуральних числах.

Узагальнення 3  теореми Ферма.  Нехай

 x^y+z^u=s^t,    (3)

де x, y, z, u, s, t – невідомі  різні натуральні числа.

Гіпотеза:  Рівняння (3) має безліч розв'язків в натуральних числах.

Узагальнення 4  теореми Ферма.  Нехай

Ax^y+Bz^u=Cs^t,    (4)

де x, y, z, u, s, t – невідомі  різні натуральні числа, A, B, C, - відомі різні натуральні числа

Гіпотеза:  Рівняння (4) має безліч розв'язків в натуральних числах.
Система діофантових рівнянь має цілочисельну трійку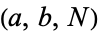  де

(1)

з відомими 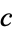 і 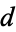 цілими числами. Приклади включають в себе

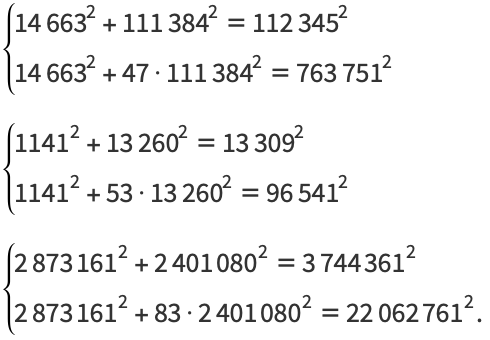(2)

Діксон (2005) стверджує, що К. Х. Брукс і С. Ватсон знайшли в "Жіночих та джентльменських щоденниках" (1857), що 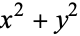і 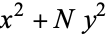можуть бути одночасно квадратами 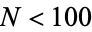лише для 1, 7, 10, 11, 17, 20, 22, 23, 24, 27, 30, 31, 34, 41, 42, 45, 49, 50, 52, 57, 58, 59, 60, 61, 68, 71, 72, 74, 76, 77, 79, 82, 85, 86, 90, 92, 93, 94, 97, 99 і 100 (які, очевидно, не містять 47, 53 і 83 зверху). Список узгоджених простих чисел менше 1000 доповнюється, за винятком 16 простих чисел 103, 131, 191, 223, 271, 311, 431, 439, 443, 593, 607, 641, 743, 821, 929 та 971.

Практична частина 

Приклад 1. Розв’язати квазіпіфагорові рівняння:
 А)4x²+7y² = 9z^{2 
на множині натуральних чисел.}

Розв’язання:

А)4x²+7y² = 9z² - це квазіпіфагорове рівняння, з коефіцієнтами: 
g=4, q=9, р=7, 
тому скористаємося відомими формулами Вінницького для запису розв'язків. Нехай  k, m – натуральні числа. 

х = (gk²-рm²)q^0,5 

y = 2kmg^0,5q^0,5  ,

z= gk²+рm².

х = 3(4k²-7m²),  де k, m -натуральні числа.

y = 2km*2*3=12km, де k, m -натуральні числа.

z= 4k²+7m²,  де k, m -натуральні числа.

Відповідь: (3(4k²-7m²); 12km; 4k²+7m²),
 де k, m -натуральні числа.

_______________________________

НАПРИКЛАД 2. Розглянемо рівняння вигляду
 x²+рy² = z²

Зрозуміло, що рівняння
  x²+рy² = z² 
має безліч цілих розв’язків    (x; y; z), якщо р – натуральне число.

Доведення. Нехай  k, m – цілі числа. Перевіримо той факт,  що

х = k²-рm²,  де   р – натуральне число;

y = 2km,  

z= k²+рm²,  де   р – натуральне число;
задовольняють дане рівняння. Для цього виконаємо тотожні перетворення:

x²+рy² = (k²-рm²)² + р(2km)²= k⁴-2рk²m²+р²m⁴+4рk²m²= k⁴+2рk²m²+4р²m⁴= (k²+рm²)² = z². Що вимагалося довести.

Приклад 3. Довести, що рівняння  x²+3y² = z² має цілі розв’язки.

Доведення. Нехай  k, m – цілі числа. Перевіримо той факт,  що

х = k²-3m², 

y = 2km,

z= k²+3m²,

задовольняють дане рівняння.

x²+3y² = (k²-3m²)² + 3(2km)²= k⁴-6k²m²+9m⁴+12k²m²= k⁴+6k²m²+9m⁴= (k²+2m²)² = z². 

НАПРИКЛАД 4. Розглянемо рівняння вигляду
 аx^k+by^k = c, де х, у - невідомі цілі числа.

Яка умова існування розв’язків для  рівняння ах^k-bу^k=с, де  а,b,с – відомі натуральні числа, які  попарно взаємно прості,  х, у – невідомі натуральні числа?   

Якщо для будь-яких натуральних чисел 

х={1;2;3;…c-1}  

і для будь-яких натуральних чисел 

y={1;2;3;…c-1} не виконується умова

ах^k-bу^k ≡ 0(mod c),

тоді рівняння ах^k-bу^k=с  немає розв’язків в натуральних числах.

Завдання 1.  Дослідити, чи цілочисельне рівняння 2х²-5у²=7 має розв’язки?

Спочатку складаємо дві таблиці для знаходження множини остач при подільності на 7 для виразів n, n², 2n², 5t², 2n²-5t ²

n(mod 7)	7k+1	7k+2	7k+3	7k+4	7k+5	7k+6
n2(mod 7)	7m+1	7m+4	7m+2	7m+1	7m+4	7m+1
2n2(mod 7)	7p+2	7p+1	7p+4	7p+2	7p+1	7p+2
5t2(mod 7)	7q+5	7q+6	7q+3	7q+5	7q+6	7q+5

2n2-5t2(mod 7)
		2n2(mod 7)
		7p+1	7p+2	7p+4
5t2(mod 7)	7q+3	7g+5	7g+6	7g+1
	7q+5	7g+3	7g+4	7g+6
	7q+6	7g+2	7g+3	7g+5

Отже,  цілочисельний вираз 2n²-5t²  при діленні 7 можна отримати різні остачі: 0; 1; 2; 3; 4; 5; 6.

Вираз 2n²-5t²  ділиться націло на 7 тоді і тільки тоді, коли цілі числа n і t кратні 7, тому  n=7u; t=7w, підставимо у дане рівняння   і отримаємо рівність:

49(2u²-5w² ) = 7, 

 ліва частина цієї рівності ділиться націло на 49, а права частина рівності не ділиться націло на 49, тобто дає остачу 7.

Висновок: Рівняння  2х²-5у²=7 в натуральних числах немає розв’язків.

Завдання 2. 

 Скільки існує розв'язків в цілих числах  х та у від 1 до 1000, для яких х²+у²=49m   ( пари (х; у) і (у; х) вважати однаковими)?

Розв’язування. Зазначимо такий факт, який обгрунтовується з властивості квадратів цілих чисел: а²=(-а)²:  якщо цілочисельна пара (х; у) задовольняє умову задачі, тоді цілочисельні пари (-х; -у); (х; -у) теж задовольняють умову задачі.  Розкладемо на прості множники число 49=7*7. Проаналізуємо ділення цілочисельного виразу  х²+у² на 7.

Подамо цілочисельні змінні х та у  у вигляді остач (лишків) при діленні на 7.

{7m-3; 7m-2; 7m-1; 7m;  7m+1; 7m+2; 7m+3 }.

Запишемо повну множину усіх  остач при діленні цілочисельного виразу  х²+у² на 7. Складемо для цього таблицю для знаходження множини остач:(тотожні перетворення виразів для отримання лишків виконайте самостійно)

х2+у2	х=7m-3	х=7m-2	х=7m-1	х=7m	х=7m+1	х=7m+2	х=7m+3
у=7k-3	7р+4	7р+6	7р+3	7р+2	7р+3	7р+6	7р+4
у=7k-2	7р+6	7р+1	7р+5	7р+4	7р+5	7р+1	7р+6
у=7k -1	7р+3	7р+5	7р+2	7р+1	7р+2	7р+5	7р+3
у=7k	7р+2	7р+4	7р+1	7р	7р+1	7р+4	7р+2
у=7k +1	7р+3	7р+5	7р+2	7р+1	7р+2	7р+5	7р+3
у=7k +2	7р+6	7р+1	7р+1	7р	7р+1	7р+4	7р+6
у=7k +3	7р+4	7р+6	7р+3	7р+2	7р+3	7р+6	7р+4

Проаналізувавши цю таблицю, маємо тільки один випадок, коли цілочисельний вираз х²+у² ділиться націло на 7, тобто х=7m,  у=7k. Таким чином, цілочисельний вираз х²+у²поділиться на 49 тоді і тільки тоді,  коли х=7m,  у=7k. 

Виконаємо на цю умову обмеження: 1<=7m<=1000, 1<=7k <=1000.  Отже, 1<=m<=142,  1<=k <=142.

Порахуємо кількість пар цілочисельних пар (х; у), враховуючи  (х; у) і (у; х) вважати однаковими:

(142*7; 142*7), (142*7; 141*7), (142*7; 140*7),    …, (142*7; 1*7),  142 пари

                            (141*7; 141*7), (141*7; 140*7),    …, (141*7; 1*7), 141 пара

                                                        (140*7; 140*7),    …, (140*7; 1*7), 140 пар

                                                                                      ……….

                                                                                               (1*7; 1*7). 
1 пара

142+141+140+…2+1= 142*143/2=10153.

Відповідь: 10153 пар.

Зауваження. Використовуючи елементи цього  доведення  можна показати, що множина рівняння х²+у²=7,  х²+у²=14,  х²+у²=21,  х²+у²=28,   х²+у²=35,  х²+у²=42,    не має розв’язків в натуральних числах.  

Завдання.

1. Вказати на логічні помилки в розв’язанні квазіпіфагорового рівняння в цілих числах:   а²+3b²=с².

 Розв’язання.
Якщо b = 0, тоді а²=с², або  а₁=с;   а₂=-с. Отже, множина цілочисельних трійок:

{ (a; b; c)|  (k; 0; k); (k; 0; -k); (-k; 0; k); (-k; 0; -k), де k – ціле число} являється розв’язком даного рівняння.

Виконаємо тотожне перетворення:

c²- a²= 3b²

(c-a)(а+с) = 3b²

з останньої рівності слідує, що цілі  числа а та с при діленні на 3 мають: або однакові остачі(цей випадок розглянули спочатку), або різні остачі

1)с=3k+1, а = 3n-1 

2)с=3k-1, а = 3n+1 

Якщо  b=3m, тоді  при умові: 1) має виконуватися рівність:

(3n-1-3k+1) (3n-1+3k-1)=3*(3m)² , тобто  9(n-k)(n+k)=27m², яка виконується для множини трійок:

{ (n; m; k)| (2;1;1); (2;-1;-1); (2;-1;1); (2; 1;-1); (-2;1;1); (-2;-1;-1); (-2;1;-1); (-2;-1;1)}.

Тому, маємо ще розв’язки виду для рівняння а²+3b²=с²:

{ (a; b; c) | (1;1;2); (1;-1;-2); (1;-1;2); (1; 1;-2); (-1;1;2); (-1;-1;-2); (-1;1;-2); (-1;-1;2)}. 

2. Спробуйте дослідити властивості розв'язків  цілочисельного рівняння: а²+рb²=с²

3. Чи завжди натуральні трійки (x; y; z)  

х = k²-рm²,  де  k,  m, р – натуральні числа;

y = 2km, де  k,  m – натуральні числа;

z= k²+рm²,  де  k,  m, р – натуральні числа

як розв’язки квазіпіфагорових рівнянь  x²+рy² = z²

являються  довжинами сторін плоского трикутника?

Гіпотеза: не завжди. Спробуйте довести чи спростувати цю гіпотезу.

4.Спробуйте  дослідити властивості розв’язків для в дечому  подібних до квазіпіфагорових цілочисельних нелінійних рівнянь: 

gx⁴+py⁴=qz⁴;      gx³+py³=qz³;          gx²+py⁴=qz⁶; 

81x⁴+3y⁴=16z⁴;    а²+5b²=с²+1;      а²+7b²=с³-1;

 а²+11b²=с³+1.  

Завдання для самостійної роботи:

1. Доведіть, що рівняння в цілих числах а²+3b²=7 має чотири розв’язки, а саме

(-2;1);   (-2;-1); (2;1); (2; -1).

2. Доведіть, що рівняння в цілих числах а²+3b²=63 має чотири розв’язки, саме

(-3;6);   (-3;-6); (3;6); (3; -6).

3. Доведіть, що рівняння в цілих числах а²+3b²=48 має шість розв’язків, а саме:

(-6;2);   (-6;-2); (6;-2); (6; 2); (0;4); (0;-4). 

Завдання для математичних олімпіад 

від Сергія Вінницького

Використайте спосіб введення натурального параметру у алгебраїчні вирази для дослідження властивостей виразу.

1.Доведіть, що існує безліч натуральних чисел а та b таких, що

значення виразу

М= b^1/3(b-1)(a+1)^-1 – b^1/3(b+1)a^-1

являється точним кубом цілого числа, проте не являється точним квадратом цілого числа.

Вказівка. Якщо n – натуральне число, то натуральними числами будуть: а=n²+n  та b=n³, а значення виразу М дорівнює  мінус одиниці.

2.Доведіть, що існує безліч натуральних чисел а та b таких, що

значення виразу  N=(a²(b-1)^-1 – 1)(0,5-0,5b^0,5)

являється точним кубом цілого числа, проте не являється точним квадратом.

Вказівка. Якщо n - натуральні числа, то натуральними числами будуть а=n +1  та b=n², а значення виразу N дорівнює     мінус одиниці.

3.Доведіть, що існує безліч натуральних чисел а та b таких, що

значення виразів  С=0,5а+0,5b  і Р=0,25 a² -0,25b²

одночасно являються точними кубами і точними квадратами цілих чисел.

Вказівка. Якщо {k;m} - натуральні числа, то натуральними числами будуть а=k⁶ + m⁶  та b= k⁶ - m⁶  , а значення виразів дорівнює С=k⁶ та   Р= k⁶m⁶.

Рівняння для математичних олімпіад

 від Серія Вінницького

1. Довести, що рівняння   (x-t)^y-(x -t)^z=x^y+z має єдиний розв’язок в натуральних числах: (x; y; z; t)=(2; 1; 1; 1).  

Вказівка. Показати, що (2-1)¹-(2-1)¹=1²⁺¹.

Показати, що не виконуються дві нерівності при натуральних змінних x>=3; y>=3; z>=3; t>=3

(x-t)^y-(x -t)^z>=2  та (x-t)^y-(x -t)^z<-2.

2. Довести, що рівняння   (x+t)^y-(x -t)^z=(x+z)^y-t має єдиний розв’язок в натуральних числах:

  (x; y; z; t)=(1; 1; 1; 1), бо (1+1)¹-(1-1)¹=2^1-1.