понеділок, 20 листопада 2017 р.

сума трьох цілих кубів a^3+b^3+c^3

Рівняння  на множині натуральних чисел:
x3+у3+z3=u3            x3+у3+z3+ (-u)3=0

має безліч розв’язків, серед яких  x; y; z;  u попарно  взаємно прості числа:
(x; y; z;  u) =  (x; y; z; (3xyz+(x+y+z)(x2 + y2 +z2 –xy–yz–xz))1/3);
а3 + b3 + c3 =  3abc + (a+b+c)(a2 + b2 +c2 –аb–bc–ac);
Міллер і Вуллетт (1955) та Гардінер та ін. (1964) досліджували цілочисельні розв’язки:
x3+у3+z3=d.

Тобто числа представляються як сума трьох (додатних  чи від’ємних) кубічних чисел .
Для загального раціонального рівняння  
A3=B3+C3+D3 

був знайдений Ейлером (Hardy 1999, с. 20-21; Dickson 2005, с. 550-554). Харді та Райт (1979, с. 199-201) дають рішення, яке може грунтуватися на тотожності, що має дві змінні:
a3(a3+b3)3 = b3(a3+b3)3 + a3(a3-2b3)3+ b3(2a3-b3)3
a3(a3+2b3)3 = a3(a3-b3)3 + b3(a3-b3)3+ b3(2a3+b3)3
Це еквівалентно загальному рішенню 3.2.2, знайденому Рамануджаном (Berndt 1994, pp. 54 і 107; Hardy 1999, pp. 11, 68 і 237; Dickson 2005, pp. 500 і 554). Часткова квадратична ідентичність форм також дала Рамануджан (Berndt 1994, p. 56)
(3x2+5xy-5y2)3+(4x2-4xy+6y2)3 +(5x2-5xy-3y2)3 = (6x2-4xy+4y2)3
8)
перший екземпляр якого дає приємне рівняння 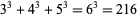3 ^ 3 + 4 ^ 3 + 5 ^ 3 = 6 ^ 3 = 216, яке є одним з номерів Платона . Такі часткові параметризації квадратичної форми можна знайти за допомогою ідентичності
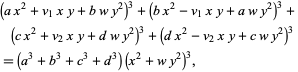(ax ^ 2 + v_1xy + bwy ^ 2) ^ 3 + (bx ^ 2-v_1xy + awy ^ 2) ^ 3 + (cx ^ 2 + v_2xy + dwy ^ 2) ^ 3 + (dx ^ 2-v_2xy + cwy ^ 2) ^ 3 = (a ^ 3 + b ^ 3 + c ^ 3 + d ^ 3) (x ^ 2 + wy ^ 2) ^ 3,
(9)
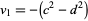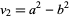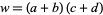де v_1 = - (c ^ 2-d ^ 2), v_2 = a ^ 2-b ^ 2і w = (a + b) (c + d), і зводиться до пошуку рішень 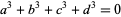a ^ 3 + b ^ 3 + c ^ 3 + d ^ 3 = 0 (або сумою може бути будь-яка кількість кубиків), що є лише окремим випадком ще більш загальної ідентичності (Piezas 2005).
22 найменших цілих рішень
3 ^ 3 + 4 ^ 3 + 5 ^ 3=6 ^ 3
(10)
1 ^ 3 + 6 ^ 3 + 8 ^ 3=9 ^ 3
(11)
3 ^ 3 + 10 ^ 3 + 18 ^ 3=19 ^ 3
(12)
7 ^ 3 + 14 ^ 3 + 17 ^ 3=20 ^ 3
(13)
4 ^ 3 + 17 ^ 3 + 22 ^ 3=25 ^ 3
(14)
18 ^ 3 + 19 ^ 3 + 21 ^ 3=28 ^ 3
(15)
11 ^ 3 + 15 ^ 3 + 27 ^ 3=29 ^ 3
(16)
2 ^ 3 + 17 ^ 3 + 40 ^ 3=41 ^ 3
(17)
6 ^ 3 + 32 ^ 3 + 33 ^ 3=41 ^ 3
(18)
16 ^ 3 + 23 ^ 3 + 41 ^ 3=44 ^ 3
(19)
3 ^ 3 + 36 ^ 3 + 37 ^ 3=46 ^ 3
(20)
27 ^ 3 + 30 ^ 3 + 37 ^ 3=46 ^ 3
(21)
29 ^ 3 + 34 ^ 3 + 44 ^ 3=53 ^ 3
(22)
12 ^ 3 + 19 ^ 3 + 53 ^ 3=54 ^ 3
(23)
15 ^ 3 + 42 ^ 3 + 49 ^ 3=58 ^ 3
(24)
22 ^ 3 + 51 ^ 3 + 54 ^ 3=67 ^ 3
(25)
36 ^ 3 + 38 ^ 3 + 61 ^ 3=69 ^ 3
(26)
7 ^ 3 + 54 ^ 3 + 57 ^ 3=70 ^ 3
(27)
14 ^ 3 + 23 ^ 3 + 70 ^ 3=71 ^ 3
(28)
34 ^ 3 + 39 ^ 3 + 65 ^ 3=72 ^ 3
(29)
38 ^ 3 + 43 ^ 3 + 66 ^ 3=75 ^ 3
(30)
31 ^ 3 + 33 ^ 3 + 72 ^ 3=76 ^ 3.
(31)
Інші невеликі рішення включають в себе
28 ^ 3 + 53 ^ 3 + 75 ^ 3=84 ^ 3
(32)
26 ^ 3 + 55 ^ 3 + 78 ^ 3=87 ^ 3
(33)
33 ^ 3 + 70 ^ 3 + 92 ^ 3=105 ^ 3
(34)
1 ^ 3 + 71 ^ 3 + 138 ^ 3=144 ^ 3
(35)
1 ^ 3 + 135 ^ 3 + 138 ^ 3=172 ^ 3
(36)
1 ^ 3 + 372 ^ 3 + 426 ^ 3=505 ^ 3
(37)
1 ^ 3 + 426 ^ 3 + 486 ^ 3=577 ^ 3
(38)
1 ^ 3 + 566 ^ 3 + 823 ^ 3=904 ^ 3
(39)
1 ^ 3 + 242 ^ 3 + 720 ^ 3=729 ^ 3
(40)
1 ^ 3 + 791 ^ 3 + 812 ^ 3=1010 ^ 3
(41)
1 ^ 3 + 236 ^ 3 + 1207 ^ 3=1210 ^ 3
(42)
1 ^ 3 + 575 ^ 3 + 2292 ^ 3=2304 ^ 3
(43)
1 ^ 3 + 1938 ^ 3 + 2820 ^ 3=3097 ^ 3
(44)
1 ^ 3 + 2676 ^ 3 + 3230 ^ 3=3753 ^ 3
(45)
1 ^ 3 + 1124 ^ 3 + 5610 ^ 3=5625 ^ 3
(46)
1 ^ 3 + 2196 ^ 3 + 5984 ^ 3=6081 ^ 3
(47)
1 ^ 3 + 1943 ^ 3 + 6702 ^ 3=6756 ^ 3
(48)
1 ^ 3 + 1851 ^ 3 + 8675 ^ 3=8703 ^ 3
(49)
(Фредкін 1972; Мадачі 1979, с. 124 і 141, голландці). База даних із сумою 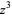z ^ 3для всіх 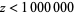z <1000000підтримується Вроблевським.
Інші загальні рішення були знайдені Бінтом (1841) і Шверінгом (1902), хоча формулювання Рамануджана є найпростішим. Немає загальних рішень, що дають усі позитивні інтегральні рішення (Dickson 2005, pp. 550-561). Ю. Кохмото знайшов 3.1.3 ^ 9рішення,
2100000 ^ 3=2046000 ^ 3 + 882000 ^ 3 + 216000 ^ 3
(50)
=1979600 ^ 3 + 1145400 ^ 3 + 85000 ^ 3
(51)
=2081100 ^ 3 + 628110 ^ 3 + 1890 ^ 3
(52)
=2043150 ^ 3 + 901200 ^ 3 + 30450 ^ 3
(53)
=2002280 ^ 3 + 1072480 ^ 3 + 30360 ^ 3
(54)
=1960480 ^ 3 + 1199520 ^ 3 + 15200 ^ 3
(55)
=1948800 ^ 3 + 1229760 ^ 3 + 30240 ^ 3
(56)
=2078160 ^ 3 + 658812 ^ 3 + 13188 ^ 3
(57)
=2009112 ^ 3 + 1048040 ^ 3 + 13888 ^ 3.
(58)
3.1.4 рівняння включають в себе
11 ^ 3 + 12 ^ 3 + 13 ^ 3 + 14 ^ 3=20 ^ 3
(59)
5 ^ 3 + 7 ^ 3 + 9 ^ 3 + 10 ^ 3=13 ^ 3.
(60)
3.1.5 включають рівняння
1 ^ 3 + 3 ^ 3 + 4 ^ 3 + 5 ^ 3 + 8 ^ 3=9 ^ 3
(61)
3 ^ 3 + 4 ^ 3 + 5 ^ 3 + 8 ^ 3 + 10 ^ 3=12 ^ 3
(62)
і рівняння 3.1.6 дається
1 ^ 3 + 5 ^ 3 + 6 ^ 3 + 7 ^ 3 + 8 ^ 3 + 10 ^ 3 = 13 ^ 3.
(63)
Рівняння 3.2.2
A ^ 3 + B ^ 3 = C ^ 3 + D ^ 3
(64)
має відомий параметричний розв'язок (Guy 1994, стор. 140; Dickson 2005, pp. 550-554), та 10 рішень із сумою 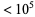<10 ^ 5,
1729 р=1 ^ 3 + 12 ^ 3 = 9 ^ 3 + 10 ^ 3
(65)
4104=2 ^ 3 + 16 ^ 3 = 9 ^ 3 + 15 ^ 3
(66)
13832=2 ^ 3 + 24 ^ 3 = 18 ^ 3 + 20 ^ 3
(67)
20683=10 ^ 3 + 27 ^ 3 = 19 ^ 3 + 24 ^ 3
(68)
32832=4 ^ 3 + 32 ^ 3 = 18 ^ 3 + 30 ^ 3
(69)
39312=2 ^ 3 + 34 ^ 3 = 15 ^ 3 + 33 ^ 3
(70)
40033=9 ^ 3 + 34 ^ 3 = 16 ^ 3 + 33 ^ 3
(71)
46683=3 ^ 3 + 36 ^ 3 = 27 ^ 3 + 30 ^ 3
(72)
64232=17 ^ 3 + 39 ^ 3 = 26 ^ 3 + 36 ^ 3
(73)
65728=12 ^ 3 + 40 ^ 3 = 31 ^ 3 + 33 ^ 3
(74)
(OEIS A001235 ; Moreau 1898). Перша цифра (Madachy 1979, с. 124 і 141) у цій послідовності, так званий номер Харді-Рамануджана , пов'язана з розповіддю про Рамануджана Г. Харді, але він був відомий ще в 1657 році (Berndt and Bhargava 1993 ) Найменше число представимо в 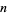ншляхах у вигляді суми кубів називається 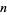нй номер таксомотора .
Рамануджан дав загальне рішення рівняння 3.2.2 як
(альфа + лямбда ^ 2гамма) ^ 3 + (лямбдабета + гама) ^ 3 = (лямбдаалфа + гама) ^ 3 + (бета + лямбда ^ 2гам) ^ 3
(75)
де
alpha ^ 2 + алфавіт + бета ^ 2 = 3lambdagamma ^ 2
(76)
(Berndt and Bhargava 1993; Berndt 1994, p. 107). Інша форма, пов'язана з Рамануджаном, - це
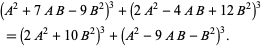(A ^ 2 + 7AB-9B ^ 2) ^ 3 + (2A ^ 2-4AB + 12B ^ 2) ^ 3 = (2A ^ 2 + 10B ^ 2) ^ 3 + (A ^ 2-9AB-B ^ 2 ) ^ 3.
(77)
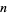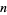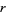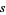Харді та Райт (1979, теорема 412) доводять, що існують числа, які можна виразити як суму двох кубів ндля кожного н(Guy 1994, с. 140-141). Доказ конструктивний, що забезпечує метод обчислення таких чисел: дані раціональні числа р і с, обчислення
т=(r (r ^ 3 + 2s ^ 3)) / (r ^ 3-s ^ 3)
(78)
ти=(s (2r ^ 3 + s ^ 3)) / (r ^ 3-s ^ 3)
(79)
проти=(t (t ^ 3-2u ^ 3)) / (t ^ 3 + u ^ 3)
(80)
ш=(u (2t ^ 3-u ^ 3)) / (t ^ 3 + u ^ 3).
(81)
Потім
r ^ 3 + s ^ 3 = t ^ 3-u ^ 3 = v ^ 3 + w ^ 3
(82)
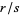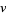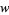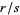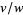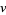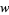У знаменників тепер можуть бути очищені , щоб зробити целочисленное рішення. Якщо г / свибрано достатньо великого, то буде позитивнимпроти і шбуде позитивним . Якщо г / свін ще більший, воно в / вбуде достатньо великим для використання протиі швикористовуватись як вхідні дані для створення третьої пари тощо. Проте ці цілі числа можуть бути досить великими, навіть для 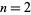n = 2. Наприклад, починаючи з 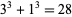3 ^ 3 + 1 ^ 3 = 28, алгоритм знаходить
28 = ((28340511) / (21446828)) ^ 3 + ((63284705) / (21446828)) ^ 3,
(83)
давати
28 · 21446828 ^ 3=(3 · 21446828) ^ 3 + 21446828 ^ 3
(84)
=28340511 ^ 3 + 63284705 ^ 3.
(85)
Цифри, представлені трьома способами, як сума двох кубів ( 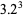3.2 ^ 3рівняння), є
87539319=167 ^ 3 + 436 ^ 3 = 228 ^ 3 + 423 ^ 3 = 255 ^ 3 + 414 ^ 3
(86)
119824488=11 ^ 3 + 493 ^ 3 = 90 ^ 3 + 492 ^ 3 = 346 ^ 3 + 428 ^ 3
(87)
143604279=111 ^ 3 + 522 ^ 3 = 359 ^ 3 + 460 ^ 3 = 408 ^ 3 + 423 ^ 3
(88)
175959000=70 ^ 3 + 560 ^ 3 = 198 ^ 3 + 552 ^ 3 = 315 ^ 3 + 525 ^ 3
(89)
327763000=300 ^ 3 + 670 ^ 3 = 339 ^ 3 + 661 ^ 3 = 510 ^ 3 + 580 ^ 3
(90)
(Guy 1994, OEIS A003825 ). Вільсон (1997) виявив 32 числа, що можна представити чотирма способами як сума двох кубів ( 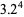3.2 ^ 4рівняння). Перше - це
6963472309248 = 2421 ^ 3 + 19083 ^ 3 = 5436 ^ 2 + 18948 ^ 3 = 10200 ^ 3 + 18072 ^ 3 = 13322 ^ 3 + 16630 ^ 3.
(91)
Найменші відомі числа, які можна представити, - 6963472309248, 12625136269928, 21131226514944, 26059452841000, ... (OEIS A003826 ). Вілсон також знайшов шість п'ятипозиційних сум,
48988659276962496 = 38787 ^ 3 + 365757 ^ 3
(92)
= 107839 ^ 3 + 362753 ^ 3
(93)
= 205292 ^ 3 + 342952 ^ 3
(94)
= 221424 ^ 3 + 336588 ^ 3
(95)
= 231518 ^ 3 + 331954 ^ 3
(96)
490593422681271000 = 48369 ^ 3 + 788631 ^ 3
(97)
= 233775 ^ 3 + 781785 ^ 3
(98)
= 285120 ^ 3 + 776070 ^ 3
(99)
= 543145 ^ 3 + 691295 ^ 3
(100)
= 579240 ^ 3 + 666630 ^ 3
(101)
6355491080314102272 = 103113 ^ 3 + 1852215 ^ 3
(102)
= 580488 ^ 3 + 1833120 ^ 3
(103)
= 788724 ^ 3 + 1803372 ^ 3
(104)
= 1150792 ^ 3 + 1690544 ^ 3
(105)
= 1462050 ^ 3 + 1478238 ^ 3
(106)
27365551142421413376 = 167751 ^ 3 + 3013305 ^ 3
(107)
= 265392 ^ 3 + 3012792 ^ 3
(108)
= 944376 ^ 3 + 2982240 ^ 3
(109)
= 1283148 ^ 3 + 2933844 ^ 3
(110)
= 1872184 ^ 3 + 2750288 ^ 3
(111)
1199962860219870469632 = 591543 ^ 3 + 10625865 ^ 3
(112)
= 935856 ^ 3 + 10624056 ^ 3
(113)
= 3330168 ^ 3 + 10516320 ^ 3
(114)
= 6601912 ^ 3 + 9698384 ^ 3
(115)
= 8387550 ^ 3 + 8480418 ^ 3
(116)
111549833098123426841016 = 1074073 ^ 3 + 48137999 ^ 3
(117)
= 8787870 ^ 3 + 48040356 ^ 3
(118)
= 13950972 ^ 3 + 47744382 ^ 3
(119)
= 24450192 ^ 3 + 45936462 ^ 3
(120)
= 33784478 ^ 3 + 41791204 ^ 3,
(121)
і єдину шестисторонню суму
8230545258248091551205888 = 11239317 ^ 3 + 201891435 ^ 3 = 17781264 ^ 3 + 201857064 ^ 3 = 63273192 ^ 3 + 199810080 ^ 3 = 85970916 ^ 3 + 196567548 ^ 3 = 125436328 ^ 3 + 184269296 ^ 3 = 159363450 ^ 3 + 161127942 ^ 3.
(122)
Рішення рівняння 3.4.4 є
2 ^ 3 + 3 ^ 3 + 10 ^ 3 + 11 ^ 3 = 1 ^ 3 + 5 ^ 3 + 8 ^ 3 + 12 ^ 3
(123)
(Мадачи 1979, с. 118 і 133).
3.6.6 також існують рівняння:
1 ^ 3 + 2 ^ 3 + 4 ^ 3 + 8 ^ 3 + 9 ^ 3 + 12 ^ 3 = 3 ^ 3 + 5 ^ 3 + 6 ^ 3 + 7 ^ 3 + 10 ^ 3 + 11 ^ 3
(124)
87 ^ 3 + 233 ^ 3 + 264 ^ 3 + 396 ^ 3 + 496 ^ 3 + 540 ^ 3
(125)
= 90 ^ 3 + 206 ^ 3 + 309 ^ 3 + 366 ^ 3 + 522 ^ 3 + 523 ^ 3.
(126)
(Мадачи 1979 р., Стор. 142; Чень Шувен).
У 1756-1757 рр. Ейлер (1761, 1849, 1915) дав параметричний розв'язок для
A ^ 3 + B ^ 3 = C ^ 2
(127)
як
А.=3n ^ 3 + 6n ^ 2-n
(128)
B=-3n ^ 3 + 6n ^ 2 + n
(129)
С=6n ^ 2 (3n ^ 2 + 1),
(130)
хоча відносно первинні рішення вимагають використання дрібних значень 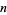н(Dickson 2005, p. 578). Щоб уникнути цього, Ейлер також дав рішення
А.=4мн (3м ^ 2-3мл + н ^ 2)
(131)
B=(mn) (3m-n) (3m ^ 2 + n ^ 2)
(132)
С=(3m ^ 2-n ^ 2) (9m ^ 4-18m ^ 3n + 18m ^ 2n ^ 2-6mn ^ 3 + n ^ 4)
(133)
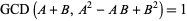за GCD (A + B, A ^ 2-AB + B ^ 2) = 1, і
А.=3м ^ 4 + 6м ^ 2н ^ 2-н ^ 4
(134)
B=-3m ^ 4 + 6m ^ 2n ^ 2 + n ^ 4
(135)
С=6мн (3м ^ 4 + п ^ 4)
(136)
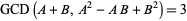для GCD (A + B, A ^ 2-AB + B ^ 2) = 3(Dickson 2005, p. 579).
Опубліковано о

Немає коментарів:

Дописати коментар

Підписатися на: Дописати коментарі (Atom)