Кватерніон в математиці
Написав Пол Бурк,червень 2001 року
Більшість шанувальників теорії чисел та класичної алгебри знайомі зі комплексними числами, тобто числами, які мають дві компоненти, ці компоненти називаються дійсними та уявними, які часто можна інтерпретувати як 2 виміри, або комплексні числа. Комплексні числа зазвичай записується як
а+ ib, де i 2 = -1, а а та b - дві величини дійсних значень.
Ця ідея може бути узагальнена на більш високі виміри, але виявляється, що 4 компоненти мають корисні властивості. Вони називаються кватерніонами і відносяться до сера Вільяма Роуана Гамільтона, який опублікував в 1844 р. Основний аналіз під назвою «Про види уявних кількостей, пов'язаних з теорією кватерніонів» у працях Королівського ірландського академії (2, с. 424-434)
У цій дискусії ми будемо писати кватерніон "Q" як
Де "r" може розглядатися як дійсне число, а "a", "b", "c" дійсні числа. 4-вимірний вектор (r, a, b, c) можна вважати вектором в 4D кватерніонному просторі.
При виконанні операцій на комплексними числами, виникає уявна одиниця: i 2, =-1', тобто відомо, що квадрат дійсного числа дорівнює -1. Існують схожі, але дещо складніші відносини між i, j, k в кватерніонному просторі. Вони такі:
| i 2 = j 2 = k 2 = -1 | ||
| ij = k | jk = i | ki = j |
| Ji = -k | kj = -i | ik = -j |
Зверніть увагу, що важливим є порядок, в якому виражається i, j, k. Також зауважте, що немає лінійних зв'язків між i, j, k.
Сума кватерніонів. Дія додавання
Додавання (або вирахування) двох кватерніонів Q 1 = r 1 + a 1 i + b 1 j + c 1 k та Q 2 = r 2 + a 2 i + b 2 j + c 2 k виконується таким чином.
Кон'югат Q = Q * = r - ai - bj - c k.
Добуток кватерніонів. Дія множення
Помноження двох кватерніонів дещо пов'язано, але безпосередньо випливає з вищезазначених зв'язків.
| Q 1 Q 2 = | [r 1 r 2 - a 1 a 2 - b 1 b 2 - c 1 c 2 ] + [r 1 a 2 + a 1 r 2 + b 1 c 2 - c 1 b 2 ] i + [r 1 b 2 + b 1 r 2 + c 1 a 2 - a 1 c 2 ] j + [r 1 c 2 + c1 r 2 + a 1 b 2 - b 1 a 2 ] k |
Зверніть увагу, що множення кватерніона не є комутативною, тобто Q 1 Q 2 НЕ така ж, як Q 2 Q 1
Довжина (модуль кватерніонів)
Довжина (величина) кватерніону - це знайома довжина координат у 4-мірному просторі.
де Q * є кон'югатом (див. пізніше), який розширюється до
і
Взаємно обернені кватерніони
Зворотний кватерніон Q -1 такий, що QQ -1 = 1 визначається як
| r - ai - bj - ck | |
| Q -1 = | ------------------------ |
| | Q | 2 |
Інверсія до нормалізованого кватерніона є просто кон'югатом, інакше величина зворотного становить 1 / | Q |. Отже, вищезгаданий вираз нормалізує кватерніон, а потім масштабів на 1 / | Q |.
Ділення кватерніонів.
Поділ Q 1 на Q 2 виглядає наступним чином
| Q 1 | Q 1 (2 r 2 - Q 2 ) | |
| -------- | = | ------------------- |
| Q 2 | | Q 2 | 2 |
Якщо m = sqrt (a 2 + b 2 + c 2 ), а v - одиничний вектор (a, b, c) / m, тоді експоненціальність кватерніону Q
Еквівалент полярних координат в кватерніонному просторі є
- r = | Q | cos (theta1)
a = | Q | гріх (theta1) cos (theta2)
b = | Q | гріх (theta1) гріх (theta2) cos (theta3)
c = | Q | гріх (тета1) гріх (тета2) гріх (тета3)
theta1 відома як амплітуда кватерніону, theta2 і theta3 - широта (або колайт) і довгота відповідно. Представницька точка кватерніону - це нормалізований вектор (a, b, c), тобто де (a, b, c) перетинається одинична сфера, центрована походженням.
Обернення вектора щодо іншого вектора
Для повороту тривимірного вектора "p" за кутовою тетою близько (одиничної) осі "r" утворюється кватерніон
і кватерніон обертання
Повернутий вектор є останніми трьома компонентами кватерніону
Легко побачити, що обертання в протилежному напрямку (-theta) можна досягти, змінивши порядок множення.
Зауважте також, що кватерніон Q 2 має одиничну величину і повинен бути для дійсного обертання.
Перетворення кватерніону до матриці
З огляду на обертання кватерніону відповідна матриця обертання 3x3 M задана значенням
| M = | 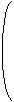 |
| 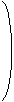 |