Вінницькі чарівні числові квадрати
Розташувати в клітинковому квадраті розміром (2k+1)x(2k+1),
k єN, послідовні
натуральні числа від 1 до (2k+1)2
так, щоб виконувалася умови:
1)
Суми чисел із двох будь-яких двох клітинок,
які симетричні відносно центральної клітинки, однакова. Тобто
f+b=i+d=h+c=j+e=s+g=…=w+n.
w
|
z
|
u
|
t
|
s
|
q
|
h
|
f
|
e
|
r
|
x
|
i
|
а
|
d
|
p
|
y
|
j
|
b
|
c
|
o
|
g
|
k
|
l
|
m
|
n
|
2)
Суми усіх чисел із клітинок, що утворюють квадратики, у яких центр симетрії
співпадає з центром симетрії центральної клітинки, однакова. Тобто 2a=b+c+d+e+f+h+i+j= k+l+n+m+o+p+r+t+s+t+u+z+w+x+y+g.
Сума чисел в зелених клітинках дорівнює сумі чисел в оранжевих клітинках і ці
суми дорівнюють числу.
Розв’язання. Розглянемо спочатку квадрат 5х5.
Розглянемо набір із 12 найменших протилежних чисел та нуля. Тобто, випишемо їх в упорядку
зростання:
-12; -11;
-10; …. -3; -2; -1; 0; 1; 2; 3; …. 10; 11; 12.
Для цих чисел виконується властивість: сума двох протилежних
дорівнює нулю. А якщо два протилежних числа розставляти в симетричних відносно центру квадрата клітинках,
то сума їх рівні нулю. Розставляємо ці
числа в даний квадрат 5х5.
ЧАРІВНИЙ КВАДРАТ 3х3 та 5х5
СЕРГІЯ ВІННИЦЬКОГО
|
||||
-9
|
-8
|
-7
|
-6
|
-5
|
-10
|
-2
|
3
|
1
|
12
|
-11
|
4
|
0
|
-4
|
11
|
-12
|
-1
|
-3
|
2
|
10
|
5
|
6
|
7
|
8
|
9
|
При такій розстановці чисел виконується умова, сума усіх
чисел в зеленому квадраті дорівнює сумі усіх чисел в оранжевому квадраті.
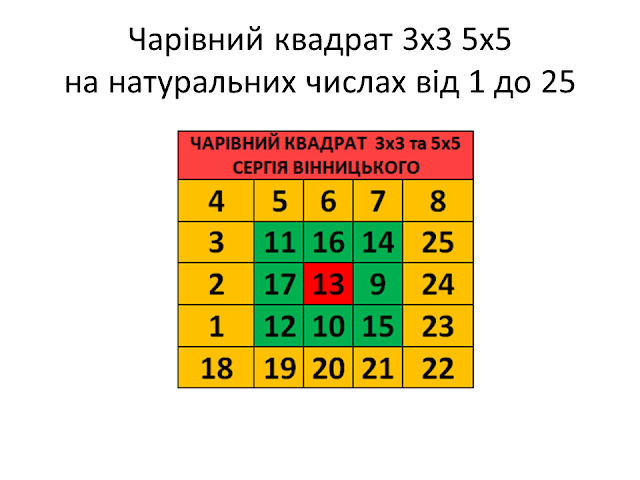
До усіх чисел цього квадрату додамо число 13. Отримаємо:
ЧАРІВНИЙ КВАДРАТ 3х3 та 5х5
СЕРГІЯ ВІННИЦЬКОГО
|
||||
4
|
5
|
6
|
7
|
8
|
3
|
11
|
16
|
14
|
25
|
2
|
17
|
13
|
9
|
24
|
1
|
12
|
10
|
15
|
23
|
18
|
19
|
20
|
21
|
22
|


Немає коментарів:
Дописати коментар